GANs とは?
GANs(Generative Adversarial Networks)は、ディープラーニングを用いた画像生成モデルの 1 つです.GANs の呼び方は、”ギャン” が一般的だとは思いますが、中には “ガン” と呼ぶ方もいたりします.ディープラーニングを用いた画像生成モデルには VAE(Variational Autoencoder)などがありますが、GANs は他の生成モデルと比べて、統計的にターゲット(訓練データ)に近い画像を生成することに成功しています.最近では、GANs を用いてハイクオリティーな “人の顔” の生成にも成功しており、世界中で大きな注目を集めています.
この動画に出ててくるのは、京大発のベンチャー企業 “データグリッド” がアイドル画像を元に、GANs で生成した “アイドルっぽい女の子” です.AKB や乃木坂 46 で見かけたような気もするハイクオリティな女の子達ですが、どの女の子も GANs によって生成されたものです.これが “統計的に” ターゲットに近い画像生成するということです.GANs の用途は画像生成のタスクに限らず、deepfake に代表されるような画像の書き換えや、物体の検知、データセットのクラスタリング、音声や脳波などの時系列信号の生成、株価の予測など幅広い分野で高い性能を発揮しています.ここまでで、ディープラーニングにおける GANs のインパクトがイメージできたと思います.
GANs の仕組み
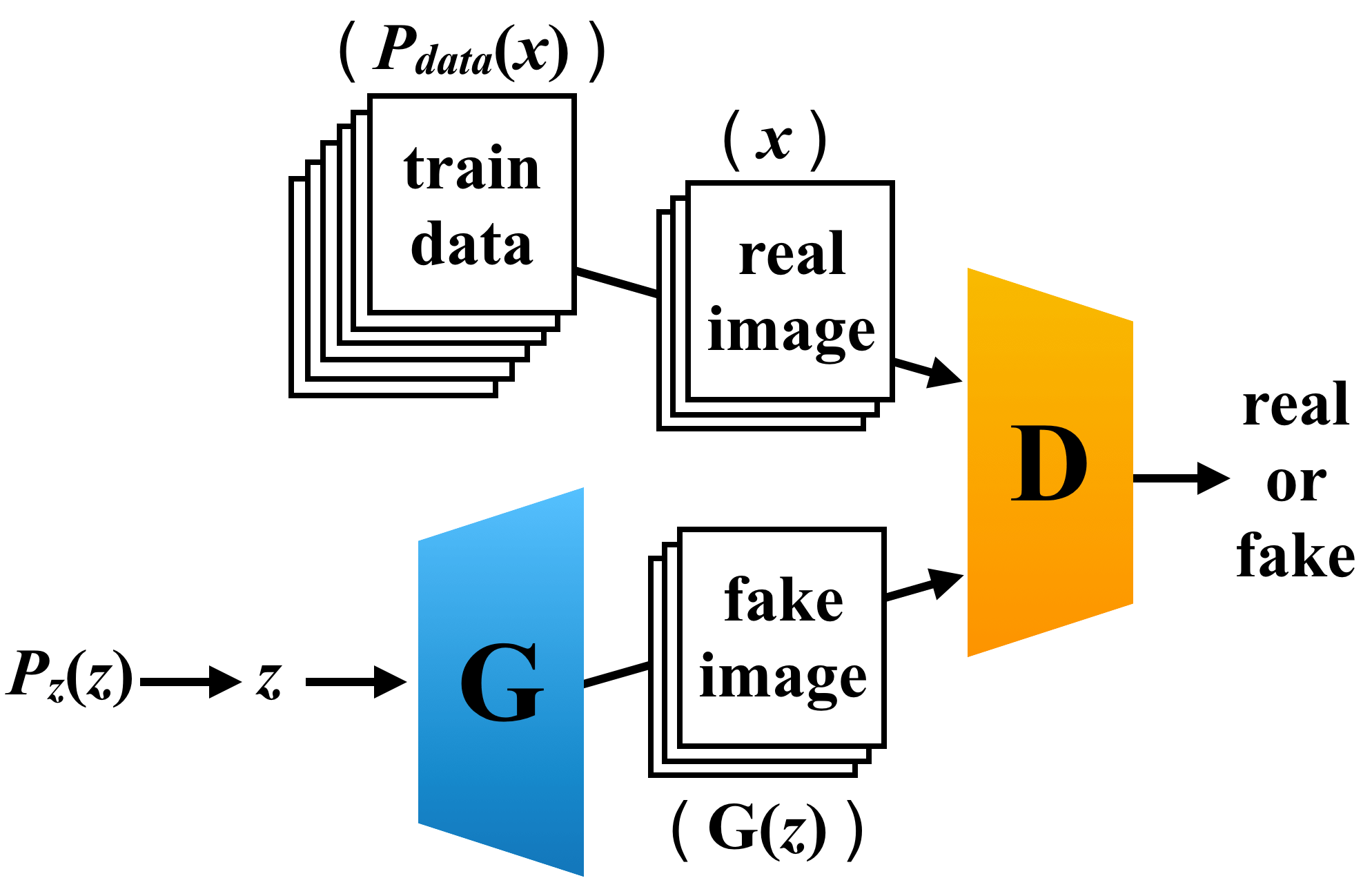
ここからは GANs がどのうようにして、ハイリアリティな画像を生成しているのかを解説していきます.GANs は Generator(G)、Discrimiantor(D)と呼ばれる 2 種類のディープラーニングモデルで構成されます.GANs は経済学や社会学、自然科学などの分野でみられる “ゲーム理論” に従って、G と D が競い合うことでターゲットに近い画像を生成していきます.GANs の概念図は以下の通りです.
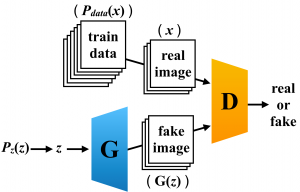
G は入力として、人工的に作られたデータ分布 \(P_z (z)\) からサンプリングされたノイズ \(z\) を受け取り、画像を生成していきます.一般的に、人工データ分布として平均 0、標準偏差 1 の ガウシアン分布 \(N[0, 1]\) が使用されています.このようにして G が生成した画像を fake 画像(\(G(z)\))とします.D は、\(P_{data} (x)\) の分布に従う訓練データからサンプリングしてきた real 画像(\(x\))か fake 画像(\(G(z)\))を入力として受け取ります.D はその入力が、real 画像なのか fake 画像なのかの真偽判定をします.G は、D が誤って real 画像と判定してしまうような巧妙な fake 画像を生成するすように訓練されます.D は、G に騙されないように、正確に真偽を判定するように訓練されます.このようにして、D と G が競い合うことで、GANs は教師なしでハイクオリティーな画像を生成することができます.
GANs のアルゴリズム
それでは、目的関数に触れながら、もう少し GANs について深掘りしていきたいと思います.GANs の目的関数は以下の数式の通りです.$$\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]$$
GANs の訓練では、G は目的関数を小さくするように最適化され、D は目的関数を大きくするように最適化されるため、前項で説明したような G と D の競争が起きます.ここで、D のタスクについて整理してみたいと思います.前項では、D は入力画像が real 画像か fake 画像かの判定をすると説明しました.少し抽象的ですよね.具体的には、D は入力画像が real 画像である確率を推定していきます.つまり、入力画像が 100% real 画像であると D が判定して場合には、D の出力は 1 、100 % fake 画像であると判定した場合には D の出力は 0 になります.ここで、D の目的関数をみてみます.D の目的関数は上記の GANs の目的関数より、
$$\max _{D} V(D, G) = \mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]$$
と、G、D それぞれの出力の対数尤度の期待値で表されます.D に real 画像 \(x\) が与えらたとき、
$$ D(x) = 1 $$
と正しく推定できていると、右辺の第 1 項が \(\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]\) は最大化されます.D に fake 画像 \(G(z)\) が与えられたとき、
$$ D(G(z)) = 0 $$
と正しく推定できていると、右辺の第 2 項\(\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]\) も最大化されます.続いて、G の目的関数についてもみてみたいと思います.G 目的関数は、
$$\min _{G} V(G, D) = \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]$$
です.G が D を上手く騙すことができていると、
$$ D(G(z)) = 1 $$
より、\(\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]\) を最小化することができます.このようにして、GANs の目的関数はミニマックス最適化されます.実際の GANs の訓練では、G の重みを固定して D を訓練し、続いて、D の重みを固定して G を訓練することで G と D は交互に訓練され、目的関数がミニマックス最適化されます(必ずしもこの順番ではない).
ここまでの解説で、GANs の目的関数と訓練アルゴリズムについて簡単に理解できたと思います.しかし、この目的関数で本当に訓練データに近い画像を生成することができるのでしょうか.もう 1 度 D の目的関数についてみてみたいと思います.
$$\max _{D} V(D, G) = \mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))]$$
D の目的関数は、ノイズの分布 \(P_z (z)\) と G から得られる生成画像のデータ分布 \(P_g\) を用いると、
$$\begin{aligned} V(D, G) &=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})[\log (1-D(G(\boldsymbol{z})))] \\ &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\ &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x \end{aligned}$$
と表されます.この式を最大化する \(D=D_{G}^{*}\) は
$$D_{G}^{*}(\boldsymbol{x})=\frac{p_{\text {data}}(\boldsymbol{x})}{p_{\text {data}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}$$
と表されます.GANs の目的関数 \(V\) に \(D_{G}^{*}\) を代入すると、
$$\begin{aligned} V(D_{G}^{*}, G) &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] \end{aligned}$$
となります.この数式はカルバックライブラー情報量(Kullback–Leibler divergence; KL)を用いて
$$\begin{aligned} V(D_{G}^{*}, G) &= \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\&= \mathbb{E}_{x \sim p_{\text {data}}}\left[\log \left(\frac{p_{\text {data}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}} \cdot \frac{1}{2}\right)\right] + \mathbb{E}_{x \sim p_{\text {g}}}\left[\log \left(\frac{p_{\text {data}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}} \cdot \frac{1}{2}\right)\right] \\& = \mathbb{E}_{x \sim p_{\text {data}}}\left[\log \left(\frac{p_{\text {data}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}}\right)+\log \left(\frac{1}{2}\right)\right] + \mathbb{E}_{x \sim p_{\text {g}}}\left[\log \left(\frac{p_{\text {g}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}}\right)+\log \left(\frac{1}{2}\right)\right] \\&= -\log 4+\mathbb{E}_{x \sim p_{\text {data}}}\left[\log \left(\frac{p_{\text {data}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}}\right)\right] +\mathbb{E}_{x \sim p_{\text {g}}}\left[\log \left(\frac{p_{\text {data}}(x)}{\frac{p_{\text {data}}(x)+p_{g}(x)}{2}}\right)\right] \\&= -\log4 + K L\left(p_{d a t a} \| \frac{p_{d a t a}+p_{g}}{2}\right) + K L\left(p_{g} \| \frac{p_{d a t a}+p_{g}}{2}\right) \end{aligned}$$
と表すことができます.この式をジェンセンシャノン情報量(Jensen-Shannon divergence; JS)を用いて書き変えると、
$$\begin{aligned}\begin{array}{c}V\left(G, D_{G}^{*}\right)=-\log 4+K L\left(p_{\text {data}} \| \frac{p_{\text {data}}+p_{g}}{2}\right)+K L\left(p_{g} \| \frac{p_{\text {data}}+p_{g}}{2}\right) \\ =-\log 4+2 \cdot J S\left(p_{\text {data}} \| p_{g}\right)\end{array}\end{aligned}$$
と表すことができます.この式は \( P_{data} = P_g \) で最小化されます.つまり、GANs の目的関数 \( V\) は、\( P_{data} = P_g \) のときに D について最大化され、G について最小化されるため、ミニマックス最適化されます.以上から、この目的関数を用いることで、GANs はノイズの分布 \(P_z (z)\) から、統計的に訓練データに近い画像を生成することができるのです.
GANs の実装とデータセット
それでは、いよいよ GANs を実装していきたいと思います.GANs を実装するにあたってこちらの example を参考にして、全て Keras で実装していきます.また今回は、DC-GAN(Deep Convolutional GAN)と cGAN(Conditional GAN)の 2 種類の GANs を実装してみたいと思います.
今回は、データセットとして CIFAR-10 を使用します.CIFAR-10 は 60,000 枚の画像と 10 個のクラスで構成されるオープンデータセットです.画像は 3 チャネル、グレイスケールの RGB 画像で、解像度は 32×32 で統一されています.クラスラベルは [0] airplane、[1] automobile、[2] bird、[3] cat、[4] deer、[5] dog、[6] frog、[7] horse、[8] ship、[9] truck の 10 種類です.CIFAR-10 の画像をクラス単位で簡単に可視化してみました.

解像度が小さいため画像はぼやけていますが、それぞれのクラスに対応したドメインをもつ画像がみて取れます.bird クラスに注目してみると、同じクラス内に背景や鳥の種類など、同一クラス内にも少しドメインが異なる画像が存在することがわかります.GAN がこれらのサンプルを上手く学習することはできるのでしょうか.CIFAR-10 は Keras でも提供されているので、わざわざデータを探してダウンロードをしなくても、簡単に利用することができます.
DC-GAN 実装
DC-GAN とは、vanilla GAN のアーキテクチャに畳み込みニューラルネットワーク(Convolutional Neural Networks; CNN)を組み込んだ GANs です.CNN については、こちらの記事で詳しく説明されているので、CNN について詳しく知りたい人はぜひ参考にしてみてください.CNN を組み込んだ以外に、DC-GAN と vanilla GAN のネットワーク構造の大きな違いはありません.DC-GAN 以降に登場した GANs には、ほとんど例外なく CNN がネットワークに組み込まれています.したがって、GANs について理解を深めていくにあたって、DC-GAN は避けることができない基本的な GANs といえます.
では、いよいよDC-GAN の実装をみていきます.G は 100 次元のノイズを入力として受け取りターゲットに近い画像を生成していきます.example と大きく異なる点は、出力層(最後の畳み込み層)のフィルタ数です.example では訓練データセットとしてグレイスケール画像のデータセットである MNIST を使用しているため、G は 1 チャネルの画像を生成するので、出力層のフィルタ数は 1 になっています.しかし、今回は CIFAR-10 を画像をターゲットとして生成していくため、出力層のフィルタ数は 3 です.また、今回は、畳み込み層から得られた特徴量マップを解像度が 2 倍となるようにアップサンプリング(nearest neighbor interpolation)することで画像を生成していきます.
def bulid_generator(latent_dim):
model = Sequential()
# 入力ノイズ: 100 --> FC 層の出力:(128*8*8) -->
#リシェイプ:(8, 8, 128) --> アップサンプリング:(16, 16, 64)
model.add(Dense(128 * 8 * 8, activation="relu", input_dim=latent_dim))
model.add(Reshape((8, 8, 128)))
model.add(UpSampling2D())
# 入力:(16, 16, 128) --> 出力:(32, 32, 128)
model.add(Conv2D(128, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(UpSampling2D())
# 入力:(32, 32, 128) --> 出力:(32, 32, 64)
model.add(Conv2D(64, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
# 入力:(32, 32, 128) --> 出力:(32, 32, 3) 生成画像
model.add(Conv2D(3, kernel_size=3, padding="same")) # RGB 画像なので出力は 3ch
model.add(Activation("tanh"))
model.summary()
noise = Input(shape=(latent_dim,))
img = model(noise)
return Model(noise, img)続いて、D の実装です.exmaple との大きな違いは入力のシェイプです.exmaple では (28, 28, 1) の画像が入力だったのに対し、今回は (32, 32, 3) の画像が入力になっています.また、画像を生成する G とは異なり、D の訓練の目標は、 “ターゲットの特徴を学習し、入力画像の真偽を正確に判定すること” であるため、入力画像を畳み込みながら入力画像の特徴量を抽出していく必要あります.したがって、stride = 2 で畳み込むことで入力のサイズを徐々に小さくしていきます.
def build_discriminator(img_shape):
model = Sequential()
# 入力:(32, 32, 3) --> 出力:(16, 16, 32)
model.add(Conv2D(32, kernel_size=3, strides=2, input_shape=(32, 32, 3), padding="same"))
model.add(LeakyReLU(alpha=0.2))
# 入力:(16, 16, 32) --> 出力:(8, 8, 64)
model.add(Conv2D(64, kernel_size=3, strides=2, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
# 入力:(8, 8, 64) --> 出力:(4, 4, 128)
model.add(Conv2D(128, kernel_size=3, strides=2, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
#入力:(4, 4, 128) --> Conv 出力:(4, 4, 256) --> falatten:(4096)
model.add(Conv2D(256, kernel_size=3, strides=1, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Flatten())
# 入力:(4096) --> 出力:(1) 真偽の判定結果
model.add(Dense(1, activation='sigmoid'))
model.summary()
img = Input(shape=img_shape)
validity = model(img)
return Model(img, validity)画像出力用の関数を用意しておきます.今回は、100 イテレーションごとに 12 づつ生成画像を可視化していきます.
def combine_images(img_dir, gen_imgs, epoch, idx, iterations):
r, c = 4, 3
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig, axs = plt.subplots(r, c)
fig.subplots_adjust(wspace=0.1, hspace=0.1)
cnt = 0
for i in range(r):
for j in range(c):
axs[i,j].imshow(gen_imgs[cnt, :,:,:])
axs[i,j].axis('off')
cnt += 1
fig.savefig(os.path.join(img_dir, "epoch_%d_iter_%d"%(epoch+1, idx+1)), bbox_inches='tight')
plt.close()def train():
# Load the dataset
# CIFAR-10 データセットをロード
# X_train:(50,000 ,32, 32, 3), X_test:(10,000, 32, 32, 3)
(X_train, _), (X_test, _) = cifar10.load_data()
# train_data:(60,000, 32, 32, 3)
train_data = np.vstack([X_train, X_test])
# Rescale -1 to 1
# 画像の輝度値を 0 -- 255 から -1 -- 1 にリサイズ
train_data = train_data.astype(np.float32) / 127.5 - 1.0
generator = bulid_generator(latent_dim)
discriminator = build_discriminator(img_shape)
optimizer = Adam(0.0002, 0.5)
discriminator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# The generator takes noise as input and generates imgs
# G は入力としてノイズを受け取り画像を生成
z = Input(shape=(latent_dim,))
img = generator(z)
# For the combined model we will only train the generator
# コンバインドモデルは G のみ訓練するため、D の重みを固定
discriminator.trainable = False
# The discriminator takes generated images as input and determines validity
# D は入力として生成画像を受け取り、真偽を判定
valid = discriminator(img)
# The combined model (stacked generator and discriminator)
# Trains the generator to fool the discriminator
# G は D を騙すように訓練される
combined = Model(z, valid)
combined.compile(loss='binary_crossentropy', optimizer=optimizer)
# Adversarial ground truths
# 画像の真偽ラベルを用意
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
# イテレーション = (60,000/32)=1,875
iterations = train_data.shape[0]/batch_size
for epoch in range(epochs):
for idx in range(int(iterations)-1):
# ---------------------
# Train Discriminator
# ---------------------
# Select a random half of images
# 訓練で使用する real 画像をランダムに選び出す
imgs = train_data[idx*batch_size : (idx+1)*batch_size]
# Sample noise and generate a batch of new images
# サンプルノイズを用意してから、そのノイズを元に G で fake 画像を生成
noise = np.random.normal(0, 1, (batch_size, latent_dim))
gen_imgs = generator.predict(noise)
# Train the discriminator (real classified as ones and generated as zeros)
# D を訓練(real 画像のラベルを 1、fake 画像のラベルは 0)
d_loss_real = discriminator.train_on_batch(imgs, valid)
d_loss_fake = discriminator.train_on_batch(gen_imgs, fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
# ---------------------
# Train Generator
# ---------------------
# Train the generator (wants discriminator to mistake images as real)
# G を訓練(D が G の生成画像を誤って real 1 と判定するように訓練される)
g_loss = combined.train_on_batch(noise, valid)
# Plot the progress
# 訓練の途中経過を出力
print ("%d [epoch : %d, D loss: %f, acc.: %.2f%%] [G loss: %f]"
% (iterations*epoch+idx+1, epoch, d_loss[0], 100*d_loss[1], g_loss))
# If at save interval => save generated image samples
# 生成画像を保存
if idx % 100 == 0:
noise = np.random.normal(0, 1, (12, latent_dim))
gen_imgs = generator.predict(noise)
gen_img = combine_images(img_dir, gen_imgs, epoch, idx, iterations)
# 訓練途中のモデルの重みを保存
gen_weights = generator.get_weights()
dis_weights = discriminator.get_weights()
np.save(os.path.join(model_dir, 'dcgan_generator_weights'), gen_weights)
np.save(os.path.join(model_dir, 'dcgan_discriminator_weights'), dis_weights)
# モデルを保存
generator.save(os.path.join(model_dir, 'dcgan_generator.h5'))
discriminator.save(os.path.join(model_dir, 'dcgan_discriminator.h5'))DC-GAN の生成画像
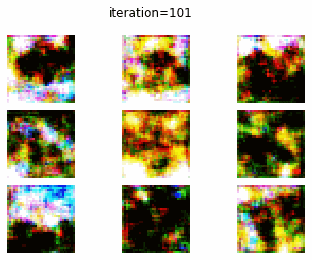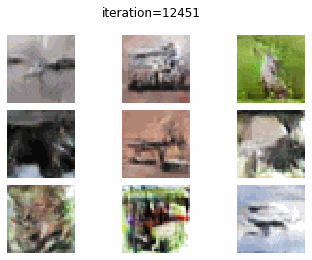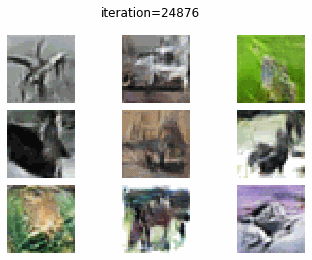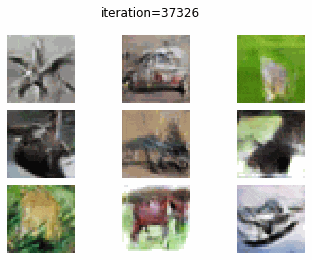
CIFAR-10 で DC-GAN を訓練した結果についてみていきます.0 エポック時点では、やはり、全くターゲットに近い画像を生成できていません.しかし、エポックが大きくなるにつれて、何かしらの物体を生成しようしていることがわかります.20 エポック訓練したときの生成画像からは、飛行機やバスらしき画像がみて取れます.しかし、まだまだ生成画像のクオリティーは低いですね.
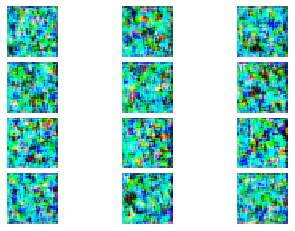
0 epoch (1 iteration)

10 epoch

20 epoch
cGAN とは
上記 DC-GAN の生成画像のクオリティは決して高いといえるもではありませんでした.これは、モデルが訓練データを十分に学習できていないためです.では、モデルが効率よくデータを学習し、生成画像のクオリティを向上させるためにはどうしたらいいでしょうか.訓練データのもつドメイン(クラス情報)をクラスラベルとしてモデルに与えることで、効率よくデータセットの情報を学習できそうですよね.
データセットのクラス情報を用いて画像を生成する GANs が cGAN です.データセットのクラス情報を GANs の訓練に用いることで、生成画像のクオリティとクラス識別性が向上し、よりリアルな画像を生成することができます. cGAN の概念図は以下の通りです.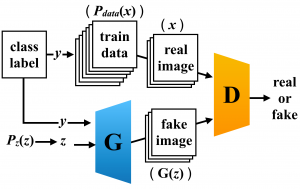
cGAN 以外にも、モデルへのクラス情報の与え方を工夫することで、様々なクラス条件付きの GANs が存在しますが、cGAN はネットワーク構造が単純であるため、クラス条件付きの GANs を理解する上での登竜門といえます.
cGAN 実装
ここから、cGAN の実装についてみていきます.cGAN の実装は example を参考にするのではなく、先ほどの DC-GAN にクラス条件を与えることで、cGAN にしていきます.
cGAN の G の実装です.G には、one-hot ベクトルでクラスラベルを与えます.具体的には、100 次元の入力ノイズに、クラスラベルの one-hot ベクトル(10 次元)を結合したものを入力としてモデルに与えます.他は DC-GAN の G と同じです.
def bulid_generator(latent_dim, class_num):
noise = Input(shape=(latent_dim,))
label = Input(shape=(class_num,), dtype='float32')
model_input = Concatenate()([noise, label])
# 入力ノイズ: 100 --> FC 層の出力:(128*8*8) -->
#リシェイプ:(8, 8, 128) --> アップサンプリング:(16, 16, 64)
hid = Dense(128 * 8 * 8, activation="relu")(model_input)
hid = Reshape((8, 8, 128))(hid)
hid = UpSampling2D()(hid)
# 入力:(16, 16, 128) --> 出力:(32, 32, 128)
hid = Conv2D(128, kernel_size=3, padding="same")(hid)
hid = BatchNormalization(momentum=0.8)(hid)
hid = Activation("relu")(hid)
hid = UpSampling2D()(hid)
# 入力:(32, 32, 128) --> 出力:(32, 32, 64)
hid = Conv2D(64, kernel_size=3, padding="same")(hid)
hid = BatchNormalization(momentum=0.8)(hid)
hid = Activation("relu")(hid)
# 入力:(32, 32, 64) --> 出力:(32, 32, 3)
hid = Conv2D(3, kernel_size=3, padding="same")(hid)
img = Activation("tanh")(hid)
return Model([noise, label], img)続いて cGAN の D です.D には、最後の畳み込み層の出力を 1 次元に平滑化したものにクラスラベルの one-hot ベクトルを結合することで、クラス情報を与えます.他は DC-GAN の D と同じです.
def build_discriminator(img_shape):
img = Input(shape=img_shape)
label = Input(shape=(class_num,), dtype='float32')
# 入力:(32, 32, 3) --> 出力:(16, 16, 32)
hid = Conv2D(32, kernel_size=3, strides=2, padding="same")(img)
hid = LeakyReLU(alpha=0.2)(hid)
# 入力:(16, 16, 32) --> 出力:(8, 8, 64)
hid = Conv2D(64, kernel_size=3, strides=2, padding="same")(hid)
hid = BatchNormalization(momentum=0.8)(hid)
hid = LeakyReLU(alpha=0.2)(hid)
# 入力:(8, 8, 64) --> 出力:(4, 4, 128)
hid = Conv2D(128, kernel_size=3, strides=2, padding="same")(hid)
hid = BatchNormalization(momentum=0.8)(hid)
hid = LeakyReLU(alpha=0.2)(hid)
# 入力:(4, 4, 128) --> Conv 出力:(4, 4, 256) --> falatten:(4096(4*4*256))
hid = Conv2D(256, kernel_size=3, strides=2, padding="same")(hid)
hid = BatchNormalization(momentum=0.8)(hid)
hid = LeakyReLU(alpha=0.2)(hid)
hid = Flatten()(hid)
# 入力:(4096), (10) --> マージ (4106)
merge = Concatenate()([hid, label])
# 入力:(4106) --> 出力:(1) 真偽の判定結果
hid = Dense(512, activation="relu")(merge)
validity = Dense(1, activation="sigmoid")(hid)
return Model([img, label], validity)def label2onehot(labels, class_num):
for i, label in enumerate(labels):
vec = np.zeros(class_num)
vec[label] = 1
if i == 0:
onehot = vec
else:
onehot = np.vstack([onehot, vec])
return onehotdef train():
# Load the dataset
# CIFAR-10 データセットをロード
(X_train, Y_train), (x_test, y_test) = cifar10.load_data() # X_train:(50,000 ,32, 32, 3), X_test:(10,000, 32, 32, 3)
train_data = np.vstack([X_train, x_test]) # train_data:(60,000, 32, 32, 3)
train_label = np.vstack([Y_train, y_test]) # train_label:(60,000, 1)
train_label = label2onehot(train_label, class_num)
# Rescale -1 to 1
# 画像の輝度値を 0 -- 255 から -1 -- 1 にリサイズ
train_data = train_data.astype(np.float32) / 127.5 - 1.0
generator = bulid_generator(latent_dim, class_num)
discriminator = build_discriminator(img_shape)
optimizer = Adam(0.0002, 0.5)
discriminator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# The generator takes noise as input and generates imgs
# G は入力としてノイズを受け取り画像を生成
z = Input(shape=(latent_dim,))
label = Input(shape=(class_num,))
img = generator([z, label])
# For the combined model we will only train the generator
# コンバインドモデルは G のみ訓練するため、D の重みを固定
discriminator.trainable = False
# The discriminator takes generated images as input and determines validity
# D は入力として生成画像を受け取り、真偽を判定
valid = discriminator([img, label])
# The combined model (stacked generator and discriminator)
# Trains the generator to fool the discriminator
# G は D を騙すように訓練される
combined = Model([z, label], valid)
combined.compile(loss='binary_crossentropy', optimizer=optimizer)
# Adversarial ground truths
# 画像の真偽ラベルを用意
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
gif_noise = np.random.normal(0, 1, (class_num, latent_dim))
gif_labels = np.identity(class_num)
stack_gif_img = []
iterations = train_data.shape[0]/batch_size
for epoch in range(epochs):
for idx in range(int(iterations)-1):
# ---------------------
# Train Discriminator
# ---------------------
# Select a random half of images
# 訓練で使用する real 画像とその画像のクラスラベルをランダムに選び出す
imgs = train_data[idx*batch_size : (idx+1)*batch_size]
labels = train_label[idx*batch_size : (idx+1)*batch_size]
# Sample noise and generate a batch of new images
# サンプルノイズを用意してから、そのノイズとクラスラベルを元に G で fake 画像を生成
noise = np.random.normal(0, 1, (batch_size, latent_dim))
gen_imgs = generator.predict([noise, labels])
# Train the discriminator (real classified as ones and generated as zeros)
# D を訓練(real 画像のラベルを 1、fake 画像のラベルは 0)
d_loss_real = discriminator.train_on_batch([imgs, labels], valid)
d_loss_fake = discriminator.train_on_batch([gen_imgs, labels], fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
# ---------------------
# Train Generator
# ---------------------
# Train the generator (wants discriminator to mistake images as real)
# G を訓練(D が G の生成画像を誤って real 1 と判定するように訓練される)
g_loss = combined.train_on_batch([noise, labels], valid)
# Plot the progress
# 訓練の途中経過を出力
print ("%d [D loss: %f, acc.: %.2f%%] [G loss: %f]" % (iterations*epoch+idx+1, d_loss[0], 100*d_loss[1], g_loss))
# If at save interval => save generated image samples
# 生成画像を保存
if idx % 100 == 0:
noise = np.random.normal(0, 1, (12, latent_dim))
labels = np.random.randint(0, class_num, 12).reshape(-1, 1)
labels = label2onehot(labels, class_num)
gen_imgs = generator.predict([noise, labels])
gen_img = combine_images(img_dir, gen_imgs, epoch, idx, iterations)
# モデルの重みを保存
gen_weights = generator.get_weights()
dis_weights = discriminator.get_weights()
np.save(os.path.join(model_dir, 'cgan_generator_weights'), gen_weights)
np.save(os.path.join(model_dir, 'cgan_discriminator_weights'), dis_weights)
# モデルを保存
generator.save(os.path.join(model_dir, 'cgan_generator.h5'))
discriminator.save(os.path.join(model_dir, 'cgan_discriminator.h5'))
makeGIF(gif_dir)cGAN の生成画像
CIFAR-10 で cGAN を訓練した結果についてみていきます.0 エポック時点では、DC-GAN と同様に、よくわからないノイズ画像しか生成できていません.しかし、10 エポック訓練時点で飛行機のような画像がみて取れますね.20 エポックでは、馬やカエル、車のような画像がみて取れます.クオリティ自体はあまり変わらないように感じますが、それぞれの画像から “クラス情報” がみて取れるようになった気もします.

0 epoch (1 iteration)

10 epoch

20 epoch
DC-GAN vs cGAN
DC-GAN、cGAN それぞれの訓練の経過を gif にして確認してみたいと思います.どちらとも、訓練が進むに連れて生成画像のクオリテイが向上していることがわかります.しかし、DC-GAN と cGAN で、生成画像のクオリティの差をあまり確認することはできませんね.
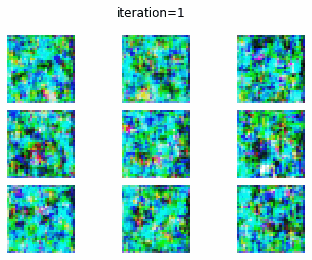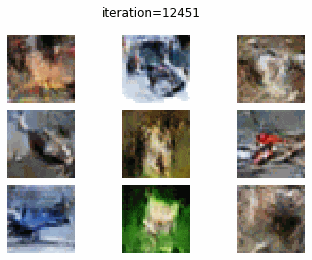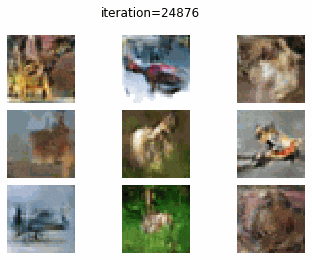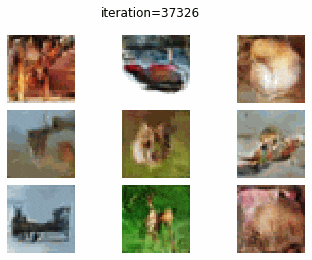
DC-GAN
cGAN
まとめ
今回は、GAN の理論について簡単に説明してから、DC-GAN と cGAN を実装して実際に画像の生成までしてみました.生成画像のクオリティはそこまで高くはありませんでしたが、中には、ターゲットに近いような画像を生成できていたので、ResBlock を用いて層を深くしたり、クラス情報の与え方などを工夫することで、クオリティを向上させることがきそうですね.この記事で紹介した GANs は、数ある GANs の中でもかなり初歩的なものです.次の記事では、cGAN の発展系であある AC-GAN や projection D を実装してみたいと思います.
高専から東京農工大学工学部に編入学し、大学時代は、画像生成ディープラーニングモデルの一種である GANs や学習済みディープラーニングモデルを用いた教師なしクラスタリング手法の研究に従事。入社 2 ヶ月で Profesional Data Engineer を取得。最近は Kaggle のメダル獲得を目標にデータサイエンスについて勉強中。



![[Google 認定資格] GCP Professional Data Engineer の勉強方法と対策](https://estyle.co.jp/media/wp-content/uploads/2020/06/1a1b6b6c416fa0e83c5039642bbcaf6a-297x300.png)




